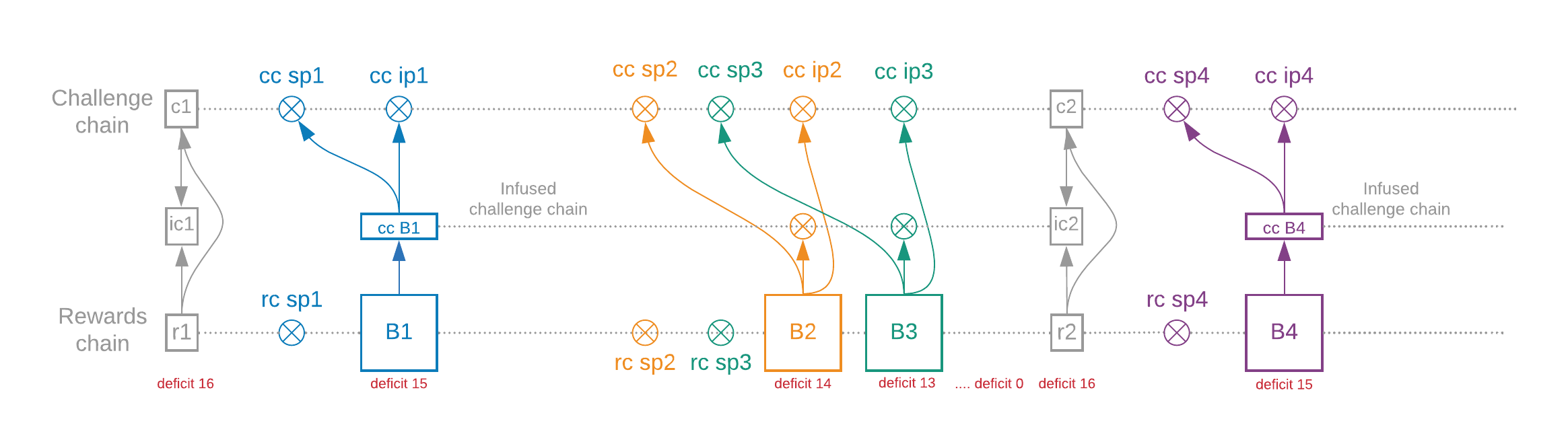
VDF chains

If we only used one VDF (for the reward chain), the inclusion or exclusion of blocks would allow control of the challenge for the next slot. This means that an attacker could try many different combinations of blocks, and choose the challenge that suits them best, to obtain more wins in the next slot.

These types of attacks are called grinding attacks, and they are one of the main difficulties of changing from Proof of Work to Proof of Space or Proof of Stake.

To mitigate this, the challenges will be based only on the first block to be infused in a slot.

There is a lot going on in this diagram! Let's break it down.

There are 4 blocks: B1, B2, B3, and B4. Farmers create these blocks. The blocks have pointers (the arrows), and the data the pointers are pointing to is all contained within the blocks themselves. At least 16 blocks have been created in the diagram's sub-slot, but we don't draw all of them due to space constraints.

The challenge chain and the reward chain each create 64 signage points, released every 2.344.69 seconds (on average) by timelords. Blocks must include the signage point VDFs (which mark the signage points) for both chains.

The timelords send their VDF output to their beacon client, which adds it into an EndOfSubSlotBundle. This bundle includes the output from each chain (for example c1, ic1, and r1 in the diagram). The bundle is propagated to all other beacon clients. Blocks must also include the infusion point VDFs for all three chains.

The challenge chain broadcasts the challenges (c1 and c2). The same chain also executes the VDF from the start of the sub-slot to the end with nothing infused into it (the circles are VDF proofs but they do not interrupt the VDF). That is, in the challenge chain, the "lottery" is completely pre-determined, and not affected by blocks in the slot, until the end of the slot.

The reward chain infuses every block that is included.

The chain in the middle is called the infused challenge chain. It starts at the first infused block for each challenge, and goes on until the end of the slot.

Recall that a slot must have at least 16 reward-chain blocks. A sub-slot doesn't have a minimum number of blocks (though it targets 32 blocks). Instead, a sub-slot always ends when sub-slot_iterations has been reached (this is targeted to take 2.5 minutes).

Because a sub-slot is targeted to produce more than 16 blocks, a slot usually only needs one sub-slot to meet its minimum-block requirement, but that is not always the case. For example, we may have only 10 blocks in a sub-slot, and then 3 and then 7, which means those three sub-slots form one slot. The deficit is the number of blocks still necessary to end the slot.

At the end of the slot, the challenge chain is combined with the infused challenge chain to generate the new challenge c2, which is used to start the challenge chain for the next sub-slot.

The only block which affects the challenge chain (and thus the PoSpace lottery) is the first block in the slot, which here is B1. In fact, it's only a deterministic part of B1 called "cc B1", which only depends on challenge chain data. An attacker who wants to grind cannot change the challenge by withholding B2, B3, or any other block apart from the first one.

An honest farmer who holds the first block (B1) will release it. If an attacker controls the first block (B1), they have two additional options: delay it or withhold it.

• Delay it: In order to know whether the new challenge will benefit them, they will need to execute the VDF all the way up to c2. By that time, their chance to get included in the reward chain is gone, since honest farmers sign only one block per proof of space.
• Withhold it: This does not provide much benefit to the attacker, since they must release it before sp2 in order to get the farmers on their chain. Farmers will choose the heaviest chain, which is the one with the most (heaviest) reward chain blocks.

Why do we commit to any blocks at all in the challenge chain? If we did not, an attacker with a faster VDF could look ahead, since they would not need the help of honest participants in order to compute the challenge chain into the future. The challenge chain would be totally deterministic. This would enable some advantage by replotting.

For a block to be considered valid, it has to provide VDFs for the challenge chain and reward chain, and optionally for the infused challenge chain if it is present. Forcing all VDFs to be included means that all three chains are guaranteed to move forward at the same rate.